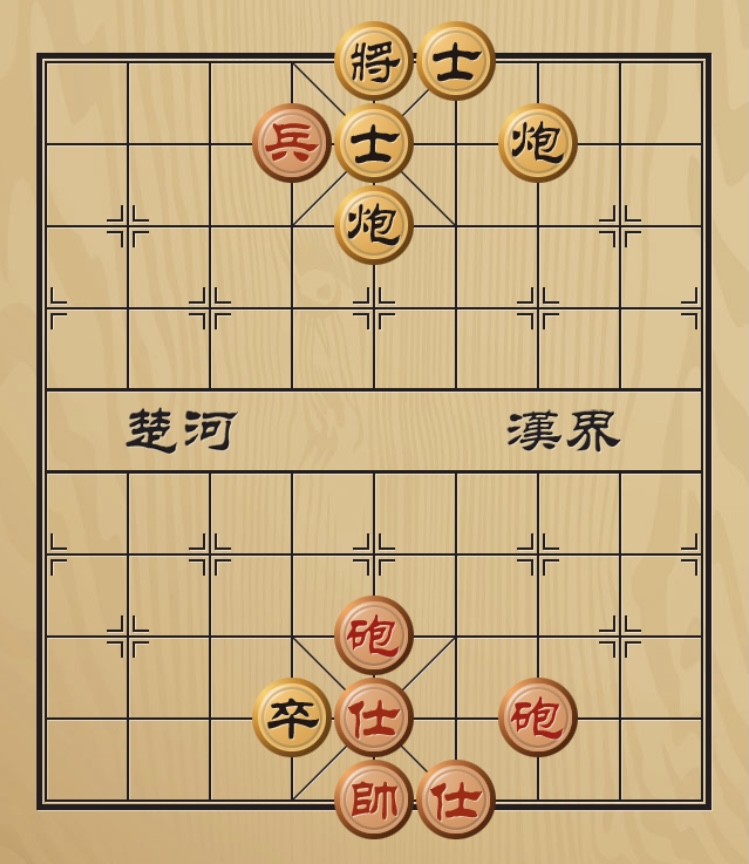
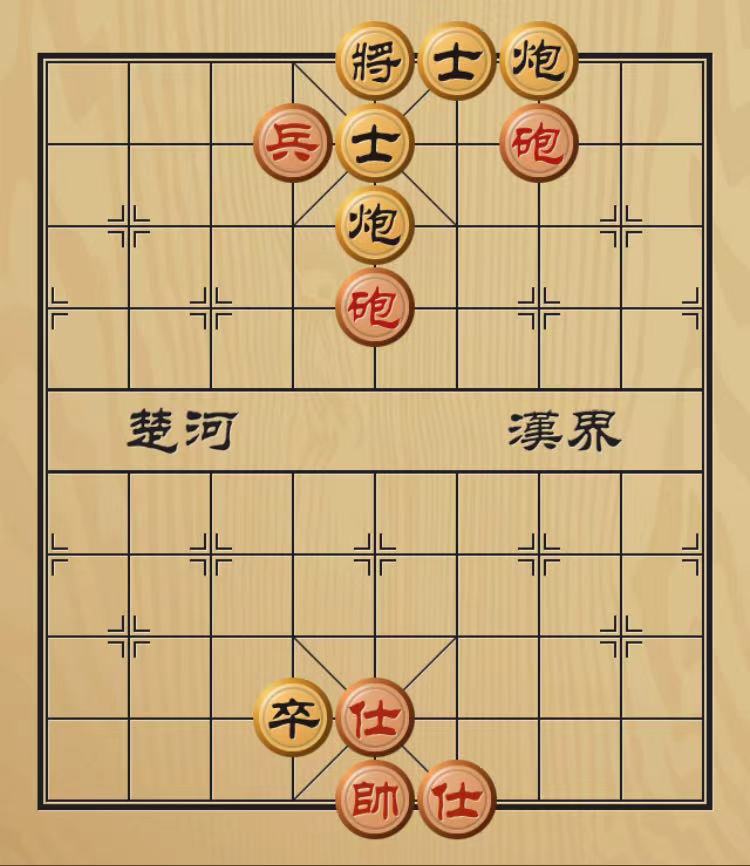
遇到一个有趣的象棋问题，如图：

图中所示红黑双方棋子数相同，但除了可以上下移动炮之外，所有棋子的移动空间都被相互锁死。 红棋最终取胜策略是用两个红炮将黑炮纵向可移动空间封死。

要想最终到达如上图红胜状态，如果红黑双方都尽最大努力博弈，从结果返推，红棋第一步最优应该走炮七进二，即使五路和七路的红黑炮之间的间距相等。 返推过程是，黑棋两个炮任一在无路可走的情况下向后只走1步。

按照这个“红黑炮”问题进行扩展：

设有\(n\)路红黑炮，中间间隔为\(\mathcal{X}=\{x_1, \ldots, x_n\}\)，且有\(x_1 \lt x_2 \lt\ldots\lt x_n\)这时红棋取胜的走法是什么？

为什么前提条件是\(x_1 \lt x_2 \lt\ldots\lt x_n\)？ 若两方是博弈智能体，尽最大可能争胜， 如\(x_n = x_{n-1}\)，那么问题将坍缩为\(n-2\)路红黑炮问题。 该递归问题队列的步长为\(2\)，所以只需讨论前几种情况。

在，

\(n=1\)时，起手红执第\(1\)路炮向前走\(x_1\)，胜。

\(n=2\)时，起手红执第\(2\)路炮向前走\((x_2 - x_1)\)步，此时\(x_2' = x_1\)，胜。

\(n=3\)时，起手红棋为防止问题坍缩为\(n=1\)（即行棋任意两路相等），设最佳执\(y\)路炮，那么需要防止出现\(x_y' \notin \{x_i\}_{i \neq y}\)，若出现，那么将\(y\)路炮走为剩余两路之差即可胜。

例1，

\(\mathcal{X}=\{8, 16, 17\}\)，则\(x_3 - x_2 = 1\)，那么红旗可直接走\(x_1\)路炮\(7\)步，胜。

例2,

\(\mathcal{X}=\{8, 16, 18\}\)，则\(x_3 - x_2 = 2\)，那么红旗可直接走\(x_1\)路炮\(6\)步，胜。